문제
상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해버렸기 때문에, 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고, 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할것이다.
목재절단기는 다음과 같이 동작한다. 먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다. 그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다. 따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. 예를 들어, 한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다. (총 7미터를 집에 들고 간다) 절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.
상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2805
알고리즘 선택
brute force로 모든 절단기 길이에 대해 나무 M개를 자르면 10^15 으로 시간초과 발생
절단기 길이를 빠르게 찾기 위해 M 범위에 대해 binary search를 적용한다. ( 1 ≤ M ≤ 2,000,000,000 (또는 나무 최대 길이) )
binary search 알고리즘 응용
1. 문제 요구사항
얻은 나무 길이 M이상을 만족하는 절단기 길이 중 최댓값 구하기
= 얻은 나무 길이 M이상을 만족하며 최소로 나무 자르기
2. 절단기 길이에 따른 얻게 되는 나무 길이 이해
cut이 절단기 길이일 때,
cut 클수록, 나무 적게 자름 -> 얻는 나무 길이 감소
cut 작을수록, 나무 많이 자름 -> 얻는 나무 길이 증가
예를들어 cut이 3, 4, 5 일 때 M을 만족한다면, cut은 나무를 적게 자르기 위해 무엇을 선택해야할까?
5를 선택해야 한다.
3. binary search의 upper bound 적용
binary search 의 uppder bound를 선택해서 문제를 풀 수 있다.
https://keepgoing0328.tistory.com/entry/%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-lowerbound-upperbound
이진 탐색 ( + 하한 lower_bound, 상한upper_bound )
이진 탐색 정렬되어 있는 데이터를 두 부분으로 나누며 값을 탐색하는 알고리즘 비슷하게 분할하는 알고리즘으로 분할정복이 있다. 하지만 분할정복은 문제를 부분적으로 해결하는 알고리즘으
keepgoing0328.tistory.com
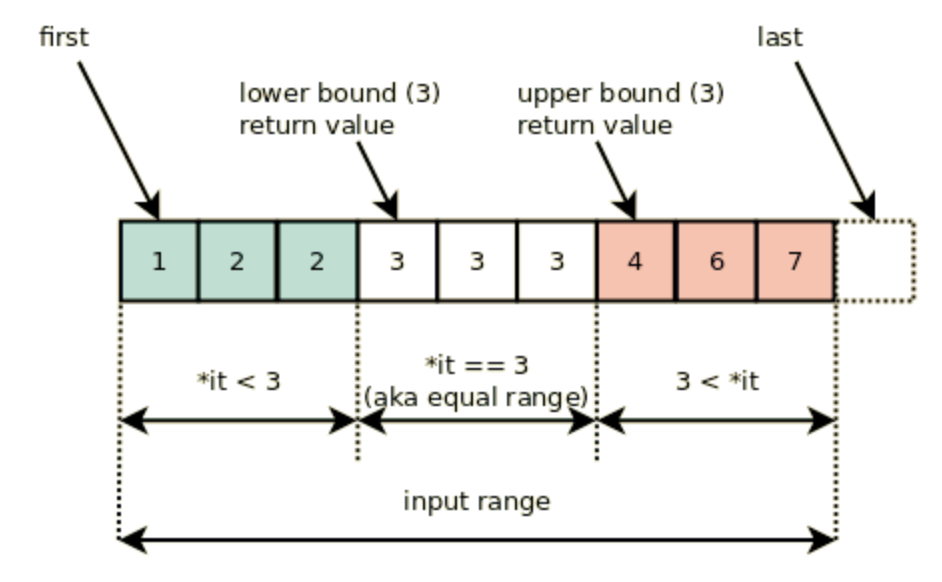
여기 binary search 에서 찾고자하는 것은 나무 전체 길이가 M인 경우의 최대 cut 길이다.
lower bound와 uppder bound 중 어떤 것을 선택할까?
lower bound 선택할 경우
- 나무 전체 길이가 처음으로 적어도 M을 만족하는 경우의 cut 을 찾게 된다.
- 이 경우 M을 만족하며 최대한 많은 나무를 자르게 된다.
uppder bound 선택할 경우
- 나무 전체 길이가 처음으로 적어도 M을 만족하는 경우 보다 커질 때의 cut을 찾게 된다.
- 따라서 cut-1을 하면 M을 만족하며 최대한 적은 나무를 자르게 된다.
따라서 정답을 찾기 위해 uppder bound 를 이용하여 적어도 M을 만족할 때의 cut 길이 구해서 1을 빼면 된다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 나무 수
N = Integer.parseInt(st.nextToken());
// 자른 나무 길이 합
M = Integer.parseInt(st.nextToken());
trees = new int[N];
st = new StringTokenizer(br.readLine());
int max = 0;
for(int i = 0 ; i < N ; i++) {
trees[i] = Integer.parseInt(st.nextToken());
if (max < trees[i]) {
max = trees[i];
}
}
find(max);
}
static int N, M;
static int[] trees;
static void find(int max) {
int min = 0;
while(min < max) {
int cut = (min + max) / 2;
// 총 길이 계산
long cutLen = getCutLen(cut);
if (cutLen >= M) {
// 총 길이가 M이라면, cut 범위를 올리기. 적게 잘라야 함
// 총 길이 M보다 큼, cut 범위를 올리기. 적게 잘라야 함
min = cut + 1;
} else {
// 총 길이 < M, cut 범위 줄이기. 더 잘라야 함
max = cut;
}
}
// 최종적으로 처음 M 보다 처음 적게 자를 때 cut이 됨
// cut - 1 처리 시 M을 만족하는 cut 범위 중 최대한 많은 나무를 자르는 길이를 구하게 됨
System.out.println(min-1);
}
static long getCutLen(int cut) {
long cutLen = 0;
for(int i = 0 ; i < N ; i++) {
int v = trees[i] - cut;
if(v <= 0) {
continue;
}
cutLen += v;
}
return cutLen;
}
}
'CS > 알고리즘 풀이' 카테고리의 다른 글
| [프로그래머스 Java]가장 많이 받은 선물 (1) | 2024.06.14 |
|---|---|
| [프로그래머스 자바] 유사 칸토어 비트열 (0) | 2024.05.27 |
| [ 백준 2003 ] 수들의 합 2 (0) | 2023.11.23 |
| [ 백준 14891 ] 톱니바퀴 ( 자바 ) (0) | 2023.04.03 |
| [ 프로그래머스 ] 종이접기 ( 자바 ) (4) | 2020.04.20 |


