https://www.acmicpc.net/problem/3020
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이 번갈아가면서 등장한다.
아래 그림은 길이가 14미터이고 높이가 5미터인 동굴이다. (예제 그림)

이 개똥벌레는 장애물을 피하지 않는다. 자신이 지나갈 구간을 정한 다음 일직선으로 지나가면서 만나는 모든 장애물을 파괴한다.
위의 그림에서 4번째 구간으로 개똥벌레가 날아간다면 파괴해야하는 장애물의 수는 총 여덟개이다. (4번째 구간은 길이가 3인 석순과 길이가 4인 석순의 중간지점을 말한다)

하지만, 첫 번째 구간이나 다섯 번째 구간으로 날아간다면 개똥벌레는 장애물 일곱개만 파괴하면 된다.
동굴의 크기와 높이, 모든 장애물의 크기가 주어진다. 이때, 개똥벌레가 파괴해야하는 장애물의 최솟값과 그러한 구간이 총 몇 개 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 H가 주어진다. N은 항상 짝수이다. (2 ≤ N ≤ 200,000, 2 ≤ H ≤ 500,000)
다음 N개 줄에는 장애물의 크기가 순서대로 주어진다. 장애물의 크기는 H보다 작은 양수이다.
풀이
메인 풀이
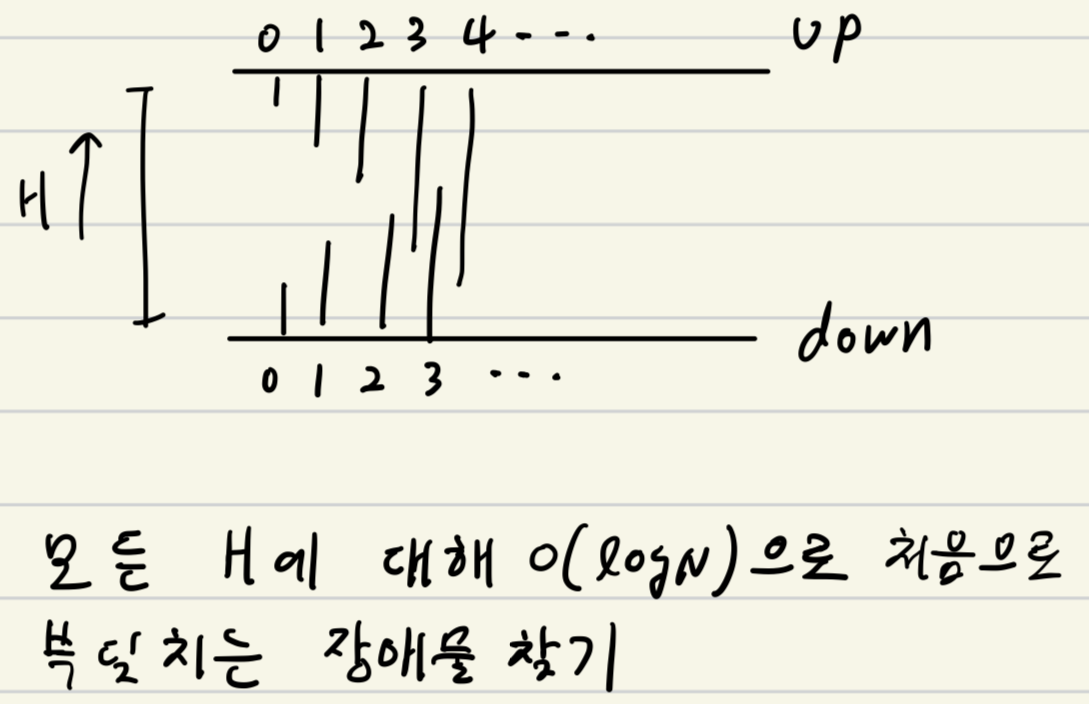
사고 과정

코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Baek3020 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int H = Integer.parseInt(st.nextToken());
int[] up = new int[N/2];
int[] down = new int[N/2];
for(int i = 0 ; i < N ; i++) {
int h = Integer.parseInt(br.readLine());
if((i & 1) == 1) {
down[i / 2] = h;
} else {
up[i / 2] = h;
}
}
Arrays.sort(up);
Arrays.sort(down);
int min = N;
int count = 0;
for (int h = 1; h <= H; h++) {
int conflicts = binarySearch(down, N / 2, h) + binarySearch(up, N / 2, H - h + 1);
if (min > conflicts) {
min = conflicts;
count = 1;
continue;
}
if (min == conflicts) {
count++;
}
}
System.out.println(min + " " + count);
}
// N - lower bound
static int binarySearch(int[] arr, int n, int targetH) {
int s = 0;
int e = n;
while(s < e) {
int mid = (s + e) / 2;
if(arr[mid] < targetH) {
s = mid + 1;
} else {
// arr[mid] >= target
e = mid;
}
}
return n - s;
}
}'CS > 알고리즘 풀이' 카테고리의 다른 글
| [PrefixSum][백준 19951] 태상이의 훈련소 생활 (0) | 2024.10.30 |
|---|---|
| [PrefixSum][백준 3020] 개똥벌레 (0) | 2024.10.26 |
| [DP 0-1 knapsack][백준 12865] 평범한 배낭 (1) | 2024.10.22 |
| [우선순위 큐][백준 1655] 가운데를 말해요 (0) | 2024.10.17 |
| [백준 9251][DP] LCS (0) | 2024.06.27 |



